Capacitors are used to “Store electrical energy” along with Resistors they make up two of the fundamental components used in electronic circuits. An ideal capacitor should have neither inductance nor resistance.
Capacitors – Use
Capacitors are used in several different ways in electronic circuits:
- Used to store charge for high-speed use or as a backup supply in case of short power-cuts
- Capacitors can also help to eliminate supply voltage ripples.
- A capacitor can block DC voltage. Any alternating current (AC) signal flows through a capacitor unimpeded.
- To filter out fast voltage changes and high-frequency signals.
- To link high-frequency signals between two circuits at different D.C. voltages.
- With a resistor to provide a time delay.
- In oscillator circuits as a timing element.
Charge and Voltage
A capacitor is an electrical component used to store energy electrostatically in an electric field between its plates. The capacitance is dictated by the surface area of the plates and the distance (and the material) between them, the closer and larger the plates the higher the capacitance.
The higher the density of charge the higher the potential difference the capacitor has across the plates.
Unlike a resistor, an ideal capacitor does not dissipate energy.
Charge Q is measured in Coulombs. 1C (=As) is the amount of charge held by 6.25×1018 electrons (electron charge: 1.6×10-19C).
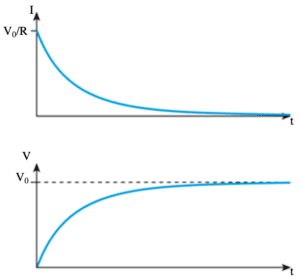
To charge a capacitor the Voltage curve can be resolved using the equation
VC = V0 (1 – e((-t)/RC))
The Current curve can be resolved using the equation
I = V0 / R e((-t)/RC)
τ=RC is the time constant of an RC-circuit
The discharge curve is the inverse.
I will cover this topic in more detail in a later post, as I suspect it is important to also cover Inductors before we go much further.




7 thoughts on “Capacitor Basics”
Nice concise description.
Might be worth expanding “store electrical energy” to explain why a capacitor is different to a battery. It’s more of an “energy reservoir” to me, than “energy storage”.
“an ideal capacitor does not dissipate energy”… but a real capacitor has a tiny resistance (that can usually be ignored).
Some people might like a sentence about super-capacitors, perhaps?
Thanks for reminding me, I will add this to posts at some point soon, but until then, I will put them here:
Trying to provide constructive feedback, as per the resistor presentation you do not provide clear explanations of the terms used in the formulae. For example there is no mention that C represents capacitance until the section calculating the capacitance.
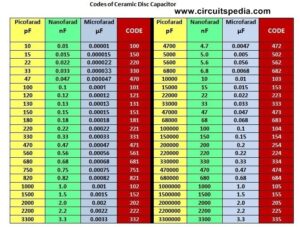
Overall there is a lot of good information in the article, in particular the chart depicting the type and usage.
There is an old adage, “do not sacrifice clarity for brevity”. For a non technical audience a little more explanation of the formulae is required.
Hi! Great work!
I would however maybe add the reference of “electrostatically stored energy” much early in the page, at the first instance you mention storing charge and add a counter to that statement “as opposed to inductors which electromagnetically store/hold charge”
That will define the category of energy storage very early on and give a comparison.
Second… the tables look backwards to me in the layout?
When looking at 1 metre broken down in nits we often see 1 m = 100 cm = 1000 mm = 1000000um = 1000000000 nm Reading from left to right.
The relationship 1 nm has to 1 m is the same as 1 nF to 1 F. Both 1 nm and 1 nF is 1e-9. 1 billionth of 1 m or 1 F
Using a scale/rule that compares the units getting smaller will help the reader visualise why a 6 digit number of capacitance may actually be a lower capacitance than a 1 digit number and most people already understand metres, centimetres and millimeters. So it can be used to visually aim the viewer.
Other than that, very interesting and good.
I hope you have a slide about why they’re one of the only parts that has not shrunk in the last 50 years.
Thanks for the idea 🙂